ソフトウェアメトリクス解説(002)
Lack of Cohesion in Methods(Henderson-Sellers)
つまり、メソッドの凝集度です。
凝 集度の測定とは、クラスやパッケージ内の機能要素と情報要素間の関連性の高さを測るものです。オブジェクト指向言語において、着目しているクラスに、互い に関連するメンバ変数とメソッドが十分に集まっている、つまり局所化されているのであれば、そのクラスのメンバ変数1つ当たりへアクセスするメソッドの数 は多くなります。
簡単にいってしまうと、メンバ変数1つ当たりへアクセスするメソッドの数が少ないとLCOM*は1へ近づき、多ければLCOM*は0へ近づきます。つまり、LCOM*の値が小さいほど凝集度が高いといえます。
LCOM*は次の式で定義されます:
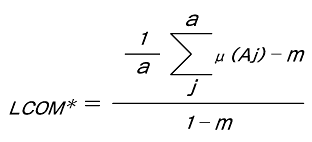
を表しています。
簡単にいってしまうと、メンバ変数1つ当たりへアクセスするメソッドの数が少ないとLCOM*は1へ近づき、多ければLCOM*は0へ近づきます。つまり、LCOM*の値が小さいほど凝集度が高いといえます。
話を具体的にするためにJavaを想定して説明しましょう。次のようなクラスを考えます。
つまり、メソッドの凝集度です。
凝 集度の測定とは、クラスやパッケージ内の機能要素と情報要素間の関連性の高さを測るものです。オブジェクト指向言語において、着目しているクラスに、互い に関連するメンバ変数とメソッドが十分に集まっている、つまり局所化されているのであれば、そのクラスのメンバ変数1つ当たりへアクセスするメソッドの数 は多くなります。
簡単にいってしまうと、メンバ変数1つ当たりへアクセスするメソッドの数が少ないとLCOM*は1へ近づき、多ければLCOM*は0へ近づきます。つまり、LCOM*の値が小さいほど凝集度が高いといえます。
LCOM*は次の式で定義されます:
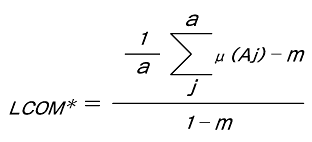
ここで、
Ajは、着目しているクラスのj番目のメンバ変数
aは、着目しているクラスのメンバ変数の個数
mは、着目しているクラスのメソッドの個数
μ(Aj)は、メンバ変数Ajにアクセスしているメソッドの個数
を表しています。
簡単にいってしまうと、メンバ変数1つ当たりへアクセスするメソッドの数が少ないとLCOM*は1へ近づき、多ければLCOM*は0へ近づきます。つまり、LCOM*の値が小さいほど凝集度が高いといえます。
話を具体的にするためにJavaを想定して説明しましょう。次のようなクラスを考えます。
class SampleClass {
private int a1, a2, a3, a4;
public void m1() {
a1=0; a2=1;
}
public void m2() {
a1=1; a2=2;
}
public void m3() {
a3=0; a4=3;
}
public void m4() {
a3=1; a4=2;
}
このとき、LCOM*の計算式に登場する各項の値は次のとおりです。
a=|A|=メンバ変数の数=4
m=|M|=メソッドの数=4
μ(a1)=a1にアクセスするメソッドの数=2
μ(a2)=a2にアクセスするメソッドの数=2
μ(a3)=a3にアクセスするメソッドの数=2
μ(a4)=a4にアクセスするメソッドの数=2
よって、このクラスのLCOM*は、
LCOM*=(((1/4) * (2+2+2+2))ー4)/(1 ? 4)=0.666……
となります。
ここでよく見てみると、{a1, a2, m1, m2}のグループと{a3, a4, m3, m4}のグループは互いに何の関係もないことが分かります。ということは、これらのグループごとにクラスを分けることによって、それぞれのグループの局所化が進み、凝集度が向上するはずです。これらのグループごとにクラスを分割した場合のLCOM*は、それぞれ次のようになります。
クラス1のLCOM*=0
クラス2のLCOM*=0
Labels: software_all

0 Comments:
Post a Comment
<< Home